The extent to which one substance will dissolve in another is determined by several factors, including the types and relative strengths of intermolecular attractive forces that may exist between the substances’ atoms, ions, or molecules. This tendency to dissolve is quantified as a substance’s solubility, its maximum concentration in a solution at equilibrium under specified conditions. A saturated solution contains solute at a concentration equal to its solubility. A supersaturated solution is one in which a solute’s concentration exceeds its solubility—a nonequilibrium (unstable) condition that will result in solute precipitation when the solution is appropriately perturbed. Miscible liquids are soluble in all proportions, and immiscible liquids exhibit very low mutual solubility. Solubilities for gaseous solutes decrease with increasing temperature, while those for most, but not all, solid solutes increase with temperature. The concentration of a gaseous solute in a solution is proportional to the partial pressure of the gas to which the solution is exposed, a relation known as Henry’s law. Properties of a solution that depend only on the concentration of solute particles are called colligative properties. The magnitudes of these properties depend only on the total concentration of solute particles in solution, not on the type of particles. The total concentration of solute particles in a solution also determines its osmotic pressure. This is the pressure that must be applied to the solution to prevent diffusion of molecules of pure solvent through a semipermeable membrane into the solution. Ionic compounds may not completely dissociate in solution due to activity effects, in which case observed colligative effects may be less than predicted.
3.1 Solubility
Learning Objectives
By the end of this section, you will be able to:
- Describe the effects of temperature and pressure on solubility
- State Henry’s law and use it in calculations involving the solubility of a gas in a liquid
- Explain the degrees of solubility possible for liquid-liquid solutions
3.1.1 Solutions of Gases in Liquids
As for any solution, the solubility of a gas in a liquid is affected by the intermolecular attractive forces between solute and solvent species. Unlike solid and liquid solutes, however, there is no solute-solute intermolecular attraction to overcome when a gaseous solute dissolves in a liquid solvent (see Figure 11.4) since the atoms or molecules comprising a gas are far separated and experience negligible interactions. Consequently, solute-solvent interactions are the sole energetic factor affecting solubility. For example, the water solubility of oxygen is approximately three times greater than that of helium (there are greater dispersion forces between water and the larger oxygen molecules) but 100 times less than the solubility of chloromethane, CHCl3 (polar chloromethane molecules experience dipole–dipole attraction to polar water molecules). Likewise note the solubility of oxygen in hexane, C6H14, is approximately 20 times greater than it is in water because greater dispersion forces exist between oxygen and the larger hexane molecules.
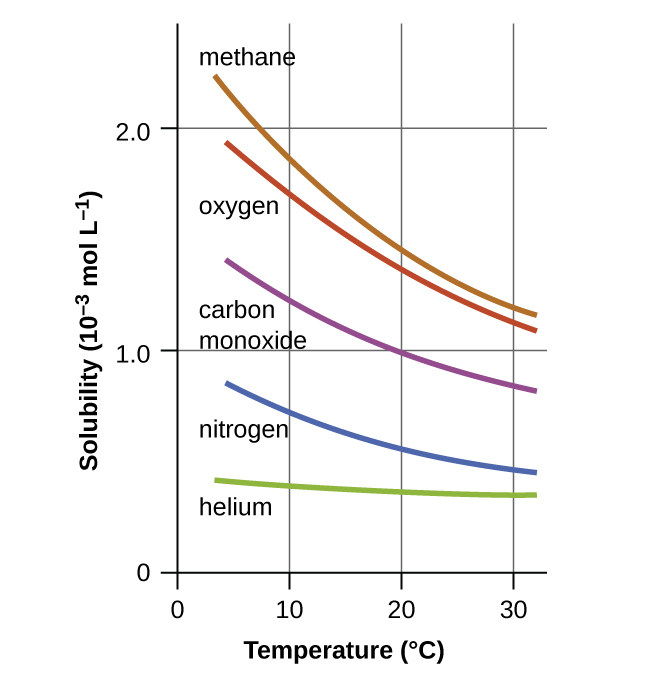
Temperature is another factor affecting solubility, with gas solubility typically decreasing as temperature increases (Figure 3.1). This inverse relation between temperature and dissolved gas concentration is responsible for one of the major impacts of thermal pollution in natural waters.
Figure 3.1
The solubilities of these gases in water decrease as the temperature increases. All solubilities were measured with a constant pressure of 101.3 kPa (1 atm) of gas above the solutions.
When the temperature of a river, lake, or stream is raised, the solubility of oxygen in the water is decreased. Decreased levels of dissolved oxygen may have serious consequences for the health of the water’s ecosystems and, in severe cases, can result in large-scale fish kills (Figure 3.2).
Figure 3.2
(a) The small bubbles of air in this glass of chilled water formed when the water warmed to room temperature and the solubility of its dissolved air decreased. (b) The decreased solubility of oxygen in natural waters subjected to thermal pollution can result in large-scale fish kills. (credit a: modification of work by Liz West; credit b: modification of work by U.S. Fish and Wildlife Service)

The solubility of a gaseous solute is also affected by the partial pressure of solute in the gas to which the solution is exposed. Gas solubility increases as the pressure of the gas increases. Carbonated beverages provide a nice illustration of this relationship. The carbonation process involves exposing the beverage to a relatively high pressure of carbon dioxide gas and then sealing the beverage container, thus saturating the beverage with CO2 at this pressure. When the beverage container is opened, a familiar hiss is heard as the carbon dioxide gas pressure is released, and some of the dissolved carbon dioxide is typically seen leaving solution in the form of small bubbles (Figure 3.3). At this point, the beverage is supersaturated with carbon dioxide and, with time, the dissolved carbon dioxide concentration will decrease to its equilibrium value and the beverage will become “flat.”
Figure 3.3
Opening the bottle of carbonated beverage reduces the pressure of the gaseous carbon dioxide above the beverage. The solubility of CO2 is thus lowered, and some dissolved carbon dioxide may be seen leaving the solution as small gas bubbles. (credit: modification of work by Derrick Coetzee)

For many gaseous solutes, the relation between solubility, Cg, and partial pressure, Pg, is a proportional one:
where k is a proportionality constant that depends on the identity of the gaseous solute, the identity of the solvent, and the solution temperature. This is a mathematical statement of Henry’s law: The quantity of an ideal gas that dissolves in a definite volume of liquid is directly proportional to the pressure of the gas.
Application of Henry’s Law
At 20 °C, the concentration of dissolved oxygen in water exposed to gaseous oxygen at a partial pressure of 101.3 kPa is 1.38
×10−3 mol L−1. Use Henry’s law to determine the solubility of oxygen when its partial pressure is 20.7 kPa, the approximate pressure of oxygen in earth’s atmosphere.Solution
According to Henry’s law, for an ideal solution the solubility,
Cg, of a gas (1.38
×10−3 mol L−1, in this case) is directly proportional to the pressure, Pg, of the undissolved gas above the solution (101.3 kPa in this case). Because both Cg and Pg are known, this relation can be rearranged and used to solve for k.Now, use k to find the solubility at the lower pressure.
Note that various units may be used to express the quantities involved in these sorts of computations. Any combination of units that yield to the constraints of dimensional analysis are acceptable.
Check Your Learning
Exposing a 100.0 mL sample of water at 0 °C to an atmosphere containing a gaseous solute at 152 torr resulted in the dissolution of 1.45
×10−3 g of the solute. Use Henry’s law to determine the solubility of this gaseous solute when its pressure is 760 torr.7.25 \(\) 10−3 in 100.0 mL or 0.0725 g/L
Thermal Pollution and Oxygen Solubility
A certain species of freshwater trout requires a dissolved oxygen concentration of 7.5 mg/L. Could these fish thrive in a thermally polluted mountain stream (water temperature is 30.0 °C, partial pressure of atmospheric oxygen is 0.17 atm)? Use the data in
Figure 3.1 to estimate a value for the Henry's law constant at this temperature.
Solution
First, estimate the Henry’s law constant for oxygen in water at the specified temperature of 30.0 °C (
Figure 3.1 indicates the solubility at this temperature is approximately ~1.2 mol/L).
Then, use this k value to compute the oxygen solubility at the specified oxygen partial pressure, 0.17 atm.
Finally, convert this dissolved oxygen concentration from mol/L to mg/L.
This concentration is lesser than the required minimum value of 7.5 mg/L, and so these trout would likely not thrive in the polluted stream.
Check Your Learning
What dissolved oxygen concentration is expected for the stream above when it returns to a normal summer time temperature of 15 °C?
3.1.4 CHEMISTRY IN EVERYDAY LIFE
Decompression Sickness or “The Bends”
Decompression sickness (DCS), or “the bends,” is an effect of the increased pressure of the air inhaled by scuba divers when swimming underwater at considerable depths. In addition to the pressure exerted by the atmosphere, divers are subjected to additional pressure due to the water above them, experiencing an increase of approximately 1 atm for each 10 m of depth. Therefore, the air inhaled by a diver while submerged contains gases at the corresponding higher ambient pressure, and the concentrations of the gases dissolved in the diver’s blood are proportionally higher per Henry’s law.
As the diver ascends to the surface of the water, the ambient pressure decreases and the dissolved gases becomes less soluble. If the ascent is too rapid, the gases escaping from the diver’s blood may form bubbles that can cause a variety of symptoms ranging from rashes and joint pain to paralysis and death. To avoid DCS, divers must ascend from depths at relatively slow speeds (10 or 20 m/min) or otherwise make several decompression stops, pausing for several minutes at given depths during the ascent. When these preventive measures are unsuccessful, divers with DCS are often provided hyperbaric oxygen therapy in pressurized vessels called decompression (or recompression) chambers (Figure 3.4). Researchers are also investigating related body reactions and defenses in order to develop better testing and treatment for decompression sicknetss. For example, Ingrid Eftedal, a barophysiologist specializing in bodily reactions to diving, has shown that white blood cells undergo chemical and genetic changes as a result of the condition; these can potentially be used to create biomarker tests and other methods to manage decompression sickness.
Deviations from Henry’s law are observed when a chemical reaction takes place between the gaseous solute and the solvent. Thus, for example, the solubility of ammonia in water increases more rapidly with increasing pressure than predicted by the law because ammonia, being a base, reacts to some extent with water to form ammonium ions and hydroxide ions.

Gases can form supersaturated solutions. If a solution of a gas in a liquid is prepared either at low temperature or under pressure (or both), then as the solution warms or as the gas pressure is reduced, the solution may become supersaturated. In 1986, more than 1700 people in Cameroon were killed when a cloud of gas almost certainly carbon dioxide bubbled from Lake Nyos (Figure 3.5) a deep lake in a volcanic crater. The water at the bottom of Lake Nyos is saturated with carbon dioxide by volcanic activity beneath the lake. It is believed that the lake underwent a turnover due to gradual heating from below the lake, and the warmer less-dense water saturated with carbon dioxide reached the surface. Consequently, tremendous quantities of dissolved CO2 were released and the colorless gas which is denser than air flowed down the valley below the lake and suffocated humans and animals living in the valley.
Figure 3.5
(a) It is believed that the 1986 disaster that killed more than 1700 people near Lake Nyos in Cameroon resulted when a large volume of carbon dioxide gas was released from the lake. (b) A CO2 vent has since been installed to help outgas the lake in a slow controlled fashion and prevent a similar catastrophe from happening in the future. (credit a: modification of work by Jack Lockwood; credit b: modification of work by Bill Evans)

3.1.5 Solutions of Liquids in Liquids
Some liquids may be mixed in any proportions to yield solutions; in other words, they have infinite mutual solubility and are said to be miscible. Ethanol, sulfuric acid, and ethylene glycol (popular for use as antifreeze, pictured in Figure 3.6) are examples of liquids that are completely miscible with water. Two-cycle motor oil is miscible with gasoline, mixtures of which are used as lubricating fuels for various types of outdoor power equipment (chainsaws, leaf blowers, and so on).
Figure 3.6
Water and antifreeze are miscible; mixtures of the two are homogeneous in all proportions. (credit: “dno1967”/Wikimedia commons)

Miscible liquids are typically those with very similar polarities. Consider for example, liquids that are polar or capable of hydrogen bonding. For such liquids, the dipole-dipole attractions (or hydrogen bonding) of the solute molecules with the solvent molecules are at least as strong as those between molecules in the pure solute or in the pure solvent. Hence, the two kinds of molecules mix easily. Likewise, nonpolar liquids are miscible with each other because there is no appreciable difference in the strengths of solute-solute, solvent-solvent, and solute-solvent intermolecular attractions. The solubility of polar molecules in polar solvents and of nonpolar molecules in nonpolar solvents is again an illustration of the chemical axiom “like dissolves like.”
Two liquids that do not mix to an appreciable extent are called immiscible. Separate layers are formed when immiscible liquids are poured into the same container. Gasoline, oil (Figure 3.7), benzene, carbon tetrachloride, some paints, and many other nonpolar liquids are immiscible with water. Relatively weak attractive forces between the polar water molecules and the nonpolar liquid molecules are not adequate to overcome much stronger hydrogen bonding between water molecules. The distinction between immiscibility and miscibility is really one of extent, so that miscible liquids are of infinite mutual solubility while liquids said to be immiscible are of very low (though not zero) mutual solubility.
Figure 3.7
Water and oil are immiscible. Mixtures of these two substances will form two separate layers with the less dense oil floating on top of the water. (credit: “Yortw”/Flickr)

Two liquids such as bromine and water that are of moderate mutual solubility are said to be partially miscible. Two partially miscible liquids usually form two layers when mixed. In the case of the bromine and water mixture, the upper layer is water, saturated with bromine, and the lower layer is bromine saturated with water. Since bromine is nonpolar, and, thus, not very soluble in water, the water layer is only slightly discolored by the bright orange bromine dissolved in it. Since the solubility of water in bromine is very low, there is no noticeable effect on the dark color of the bromine layer (Figure 3.8).
Figure 3.8
Bromine (the deep orange liquid on the left) and water (the clear liquid in the middle) are partially miscible. The top layer in the mixture on the right is a saturated solution of bromine in water; the bottom layer is a saturated solution of water in bromine. (credit: Paul Flowers)

3.1.6 Solutions of Solids in Liquids
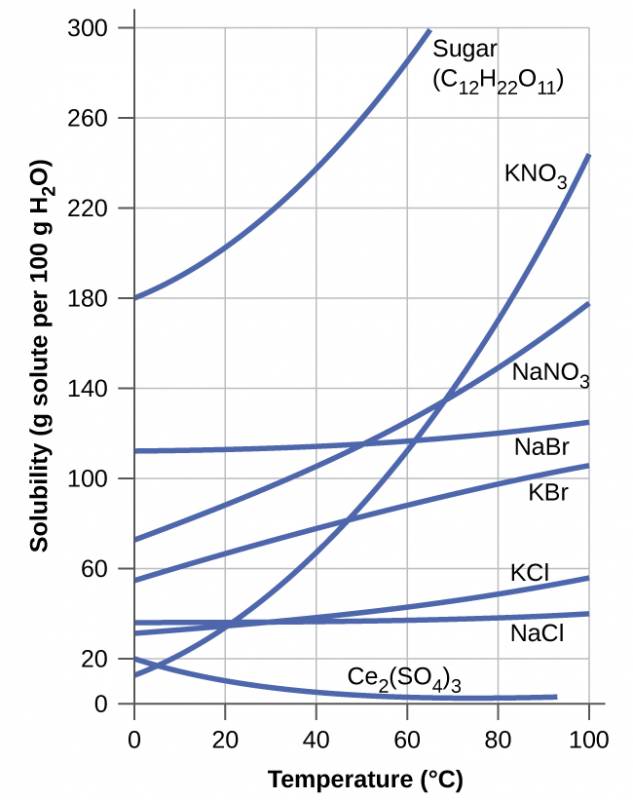
The dependence of solubility on temperature for a number of solids in water is shown by the solubility curves in Figure 3.9. Reviewing these data indicates a general trend of increasing solubility with temperature, although there are exceptions as illustrated by the ionic compound cerium sulfate.
Figure 3.9
This graph shows how the solubility of several solids changes with temperature.
The temperature dependence of solubility can be exploited to prepare supersaturated solutions of certain compounds. A solution may be saturated with the compound at an elevated temperature (where the solute is more soluble) and subsequently cooled to a lower temperature without precipitating the solute. The resultant solution contains solute at a concentration greater than its equilibrium solubility at the lower temperature (i.e., it is supersaturated) and is relatively stable. Precipitation of the excess solute can be initiated by adding a seed crystal (see the video in the Link to Learning earlier in this module) or by mechanically agitating the solution. Some hand warmers such as the one pictured in Figure 3.10 take advantage of this behavior.
Figure 3.10
This hand warmer produces heat when the sodium acetate in a supersaturated solution precipitates. Precipitation of the solute is initiated by a mechanical shockwave generated when the flexible metal disk within the solution is “clicked.” (credit: modification of work by “Velela”/Wikimedia Commons)

This video shows the crystallization process occurring in a hand warmer.
3.2 Colligative Properties
By the end of this section, you will be able to:
- Express concentrations of solution components using mole fraction and molality.
- Describe the effect of solute concentration on various solution properties.
- Explain the process of osmosis and describe how it is applied industrially and in nature.
The properties of a solution are different from those of either the pure solute(s) or solvent. Many solution properties are dependent upon the chemical identity of the solute. Compared to pure water, a solution of hydrogen chloride is more acidic, a solution of ammonia is more basic, a solution of sodium chloride is more dense, and a solution of sucrose is more viscous. There are a few solution properties however, that depend only upon the total concentration of solute species regardless of their identities. These colligative properties include vapor pressure lowering, boiling point elevation, freezing point depression, and osmotic pressure. This small set of properties is of central importance to many natural phenomena and technological applications as will be described in this module.
3.2.1 Mole Fraction and Molality
Several units commonly used to express the concentrations of solution components were introduced in an earlier chapter of this text, each providing certain benefits for use in different applications. For example, molarity (M) is a convenient unit for use in stoichiometric calculations, since it is defined in terms of the molar amounts of solute species:
Because solution volumes vary with temperature, molar concentrations will likewise vary. When expressed as molarity, the concentration of a solution with identical numbers of solute and solvent species will be different at different temperatures, due to the contraction/expansion of the solution. More appropriate for calculations involving many colligative properties are mole-based concentration units whose values are not dependent on temperature. Two such units are mole fraction (introduced in the previous chapter on gases) and molality.
The mole fraction, X, of a component is the ratio of its molar amount to the total number of moles of all solution components:
By this definition, the sum of mole fractions for all solution components (the solvent and all solutes) is equal to one.
Molality is a concentration unit defined as the ratio of the numbers of moles of solute to the mass of the solvent in kilograms:
Since these units are computed using only masses and molar amounts, they do not vary with temperature and thus, are better suited for applications requiring temperature-independent concentrations including several colligative properties, as will be described in this chapter module.
Calculating Mole Fraction and Molality
The antifreeze in most automobile radiators is a mixture of equal volumes of ethylene glycol and water with minor amounts of other additives that prevent corrosion. What are the (a) mole fraction and (b) molality of ethylene glycol, C
2H
4(OH)
2, in a solution prepared from 2.22
\(\) 10
3 g of ethylene glycol and 2.00
\(\) 10
3 g of water (approximately 2 L of glycol and 2 L of water)?
Solution
(a) The mole fraction of ethylene glycol may be computed by first deriving molar amounts of both solution components and then substituting these amounts into the definition of mole fraction.
Notice that mole fraction is a dimensionless property, being the ratio of properties with identical units (moles).
(b) Derive moles of solute and mass of solvent (in kg).
First, use the given mass of ethylene glycol and its molar mass to find the moles of solute:
Then, convert the mass of the water from grams to kilograms:
Finally, calculate molality per its definition:
Check Your Learning
What are the mole fraction and molality of a solution that contains 0.850 g of ammonia, NH
3, dissolved in 125 g of water?
7.14 \(\) 10−3; 0.399 m
Converting Mole Fraction and Molal Concentrations
Calculate the mole fraction of solute and solvent in a 3.0
m solution of sodium chloride.
Solution
Converting from one concentration unit to another is accomplished by first comparing the two unit definitions. In this case both units have the same numerator (moles of solute) but different denominators. The provided molal concentration may be written as:
The numerator for this solution’s mole fraction is, therefore, 3.0 mol NaCl. The denominator may be computed by deriving the molar amount of water corresponding to 1.0 kg
and then substituting these molar amounts into the definition for mole fraction.
Check Your Learning
The mole fraction of iodine, I
2, dissolved in dichloromethane, CH
2Cl
2, is 0.115. What is the molal concentration,
m, of iodine in this solution?
Molality and Molarity Conversions
Intravenous infusion of a 0.556
M aqueous solution of glucose (density of 1.04 g/mL) is part of some post-operative recovery therapies. What is the molal concentration of glucose in this solution?
Solution
The provided molal concentration may be explicitly written as:
Consider the definition of molality:
The amount of glucose in 1-L of this solution is 0.556 mol, so the mass of water in this volume of solution is needed.
First, compute the mass of 1.00 L of the solution:
This is the mass of both the water and its solute, glucose, and so the mass of glucose must be subtracted. Compute the mass of glucose from its molar amount:
Subtracting the mass of glucose yields the mass of water in the solution:
Finally, the molality of glucose in this solution is computed as:
Check Your Learning
Nitric acid, HNO
3(aq), is commercially available as a 33.7 m aqueous solution (density = 1.35 g/mL). What is the molarity of this solution?
3.2.5 Osmosis and Osmotic Pressure of Solutions
A number of natural and synthetic materials exhibit selective permeation, meaning that only molecules or ions of a certain size, shape, polarity, charge, and so forth are capable of passing through (permeating) the material. Biological cell membranes provide elegant examples of selective permeation in nature while dialysis tubing used to remove metabolic wastes from blood is a more simplistic technological example. Regardless of how they may be fabricated, these materials are generally referred to as semipermeable membranes.
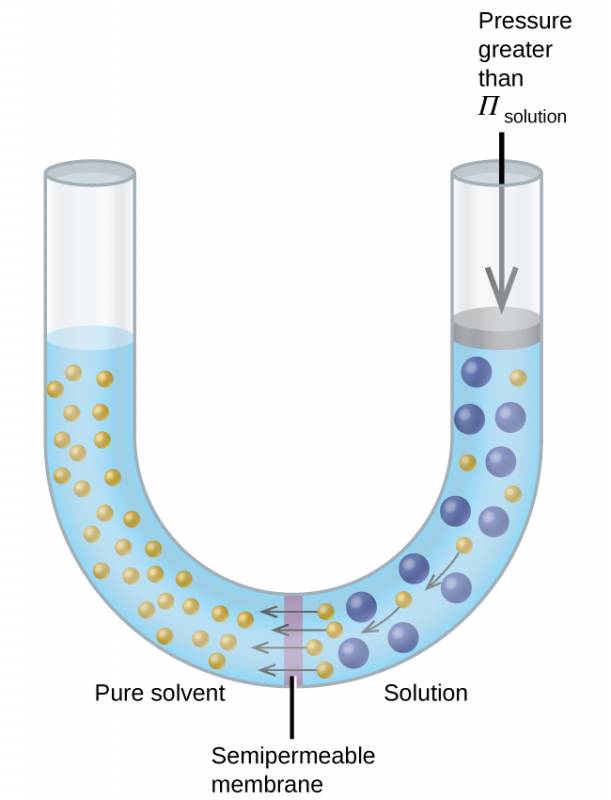
Consider the apparatus illustrated in Figure 3.11, in which samples of pure solvent and a solution are separated by a membrane that only solvent molecules may permeate. Solvent molecules will diffuse across the membrane in both directions. Since the concentration of solvent is greater in the pure solvent than the solution, these molecules will diffuse from the solvent side of the membrane to the solution side at a faster rate than they will in the reverse direction. The result is a net transfer of solvent molecules from the pure solvent to the solution. Diffusion-driven transfer of solvent molecules through a semipermeable membrane is a process known as osmosis.
Figure 3.11
(a) A solution and pure solvent are initially separated by an osmotic membrane. (b) Net transfer of solvent molecules to the solution occurs until its osmotic pressure yields equal rates of transfer in both directions.
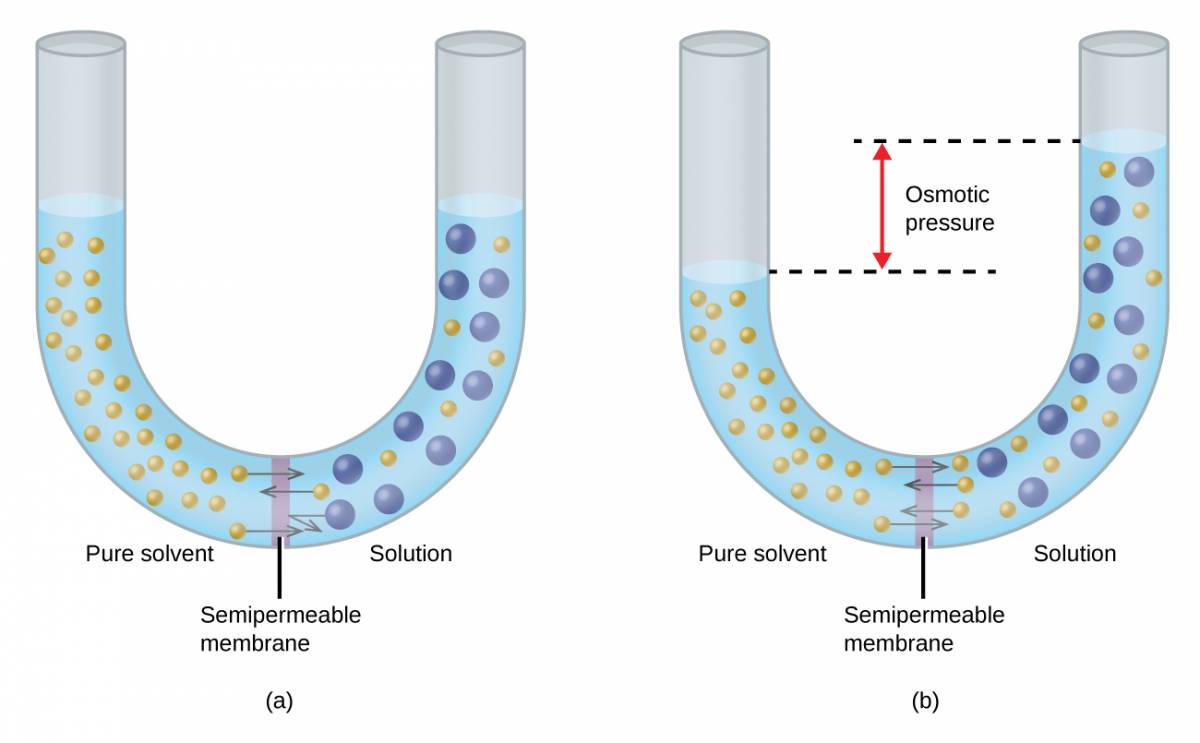
When osmosis is carried out in an apparatus like that shown in Figure 3.11, the volume of the solution increases as it becomes diluted by accumulation of solvent. This causes the level of the solution to rise, increasing its hydrostatic pressure (due to the weight of the column of solution in the tube) and resulting in a faster transfer of solvent molecules back to the pure solvent side. When the pressure reaches a value that yields a reverse solvent transfer rate equal to the osmosis rate, bulk transfer of solvent ceases. This pressure is called the osmotic pressure (Π) of the solution. The osmotic pressure of a dilute solution is related to its solute molarity, M, and absolute temperature, T, according to the equation
where R is the universal gas constant.
Calculation of Osmotic Pressure
Assuming ideal solution behavior, what is the osmotic pressure (atm) of a 0.30
M solution of glucose in water that is used for intravenous infusion at body temperature, 37 °C?
Solution
Find the osmotic pressure,
Π, using the formula
Π =
MRT, where
T is on the Kelvin scale (310 K) and the value of
R is expressed in appropriate units (0.08206 L atm/mol K).
Check Your Learning
Assuming ideal solution behavior, what is the osmotic pressure (atm) a solution with a volume of 0.750 L that contains 5.0 g of methanol, CH
3OH, in water at 37 °C?
If a solution is placed in an apparatus like the one shown in Figure 3.12, applying pressure greater than the osmotic pressure of the solution reverses the osmosis and pushes solvent molecules from the solution into the pure solvent. This technique of reverse osmosis is used for large-scale desalination of seawater and on smaller scales to produce high-purity tap water for drinking.
Figure 3.12
Applying a pressure greater than the osmotic pressure of a solution will reverse osmosis. Solvent molecules from the solution are pushed into the pure solvent.
3.2.7 CHEMISTRY IN EVERYDAY LIFE
Reverse Osmosis Water Purification
In the process of osmosis, diffusion serves to move water through a semipermeable membrane from a less concentrated solution to a more concentrated solution. Osmotic pressure is the amount of pressure that must be applied to the more concentrated solution to cause osmosis to stop. If greater pressure is applied, the water will go from the more concentrated solution to a less concentrated (more pure) solution. This is called reverse osmosis. Reverse osmosis (RO) is used to purify water in many applications, from desalination plants in coastal cities, to water-purifying machines in grocery stores (Figure 3.13), and smaller reverse-osmosis household units. With a hand-operated pump, small RO units can be used in third-world countries, disaster areas, and in lifeboats. Our military forces have a variety of generator-operated RO units that can be transported in vehicles to remote locations.
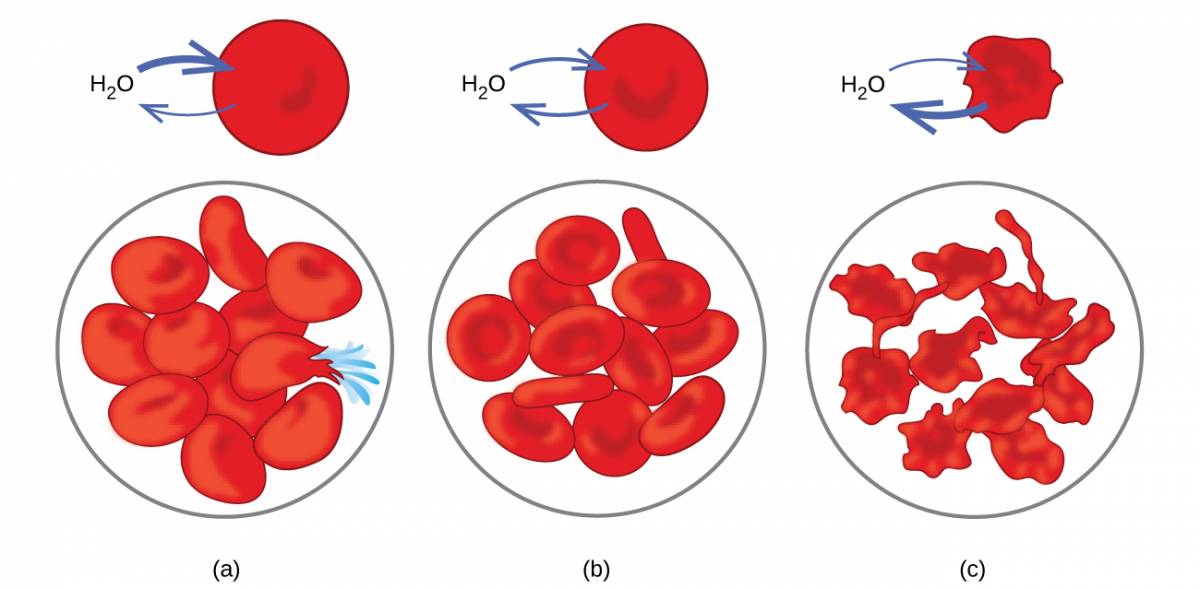
Examples of osmosis are evident in many biological systems because cells are surrounded by semipermeable membranes. Carrots and celery that have become limp because they have lost water can be made crisp again by placing them in water. Water moves into the carrot or celery cells by osmosis. A cucumber placed in a concentrated salt solution loses water by osmosis and absorbs some salt to become a pickle. Osmosis can also affect animal cells. Solute concentrations are particularly important when solutions are injected into the body. Solutes in body cell fluids and blood serum give these solutions an osmotic pressure of approximately 7.7 atm. Solutions injected into the body must have the same osmotic pressure as blood serum; that is, they should be isotonic with blood serum. If a less concentrated solution, a hypotonic solution is injected in sufficient quantity to dilute the blood serum, water from the diluted serum passes into the blood cells by osmosis, causing the cells to expand and rupture. This process is called hemolysis. When a more concentrated solution, a hypertonic solution, is injected, the cells lose water to the more concentrated solution, shrivel, and possibly die in a process called crenation. These effects are illustrated in Figure 3.14.
Figure 3.14
Red blood cell membranes are water permeable and will (a) swell and possibly rupture in a hypotonic solution; (b) maintain normal volume and shape in an isotonic solution; and (c) shrivel and possibly die in a hypertonic solution. (credit a/b/c: modifications of work by “LadyofHats”/Wikimedia commons)
3.2.8 Determination of Molar Masses
Osmotic pressure and changes in freezing point, boiling point, and vapor pressure are directly proportional to the number of solute species present in a given amount of solution. Consequently, measuring one of these properties for a solution prepared using a known mass of solute permits determination of the solute’s molar mass.
Determination of a Molar Mass from a Freezing Point Depression
A solution of 4.00 g of a nonelectrolyte dissolved in 55.0 g of benzene is found to freeze at 2.32 °C. Assuming ideal solution behavior, what is the molar mass of this compound?
Solution
Solve this problem using the following steps.
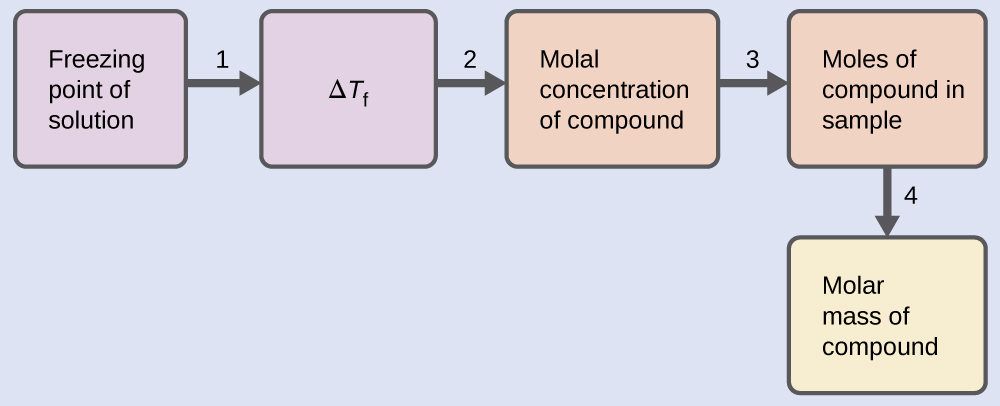
- Step 1. Determine the change in freezing point from the observed freezing point and the freezing point of pure benzene (Table 11.2).
- Step 2. Determine the molal concentration from Kf, the freezing point depression constant for benzene (Table 11.2), and ΔTf.
- Step 3. Determine the number of moles of compound in the solution from the molal concentration and the mass of solvent used to make the solution.
- Step 4. Determine the molar mass from the mass of the solute and the number of moles in that mass.
Check Your Learning
A solution of 35.7 g of a nonelectrolyte in 220.0 g of chloroform has a boiling point of 64.5 °C. Assuming ideal solution behavior, what is the molar mass of this compound?
EXAMPLE 3.2.10
Determination of a Molar Mass from Osmotic Pressure
A 0.500 L sample of an aqueous solution containing 10.0 g of hemoglobin has an osmotic pressure of 5.9 torr at 22 °C. Assuming ideal solution behavior, what is the molar mass of hemoglobin?
Solution
Here is one set of steps that can be used to solve the problem:

- Step 1. Convert the osmotic pressure to atmospheres, then determine the molar concentration from the osmotic pressure.
- Step 2. Determine the number of moles of hemoglobin in the solution from the concentration and the volume of the solution.
- Step 3. Determine the molar mass from the mass of hemoglobin and the number of moles in that mass.
Check Your Learning
Assuming ideal solution behavior, what is the molar mass of a protein if a solution of 0.02 g of the protein in 25.0 mL of solution has an osmotic pressure of 0.56 torr at 25 °C?
3.2.12 Colligative Properties of Electrolytes
As noted previously in this module, the colligative properties of a solution depend only on the number not on the identity of solute species dissolved. The concentration terms in the equations for various colligative properties (freezing point depression, boiling point elevation, osmotic pressure) pertain to all solute species present in the solution. For the solutions considered thus far in this chapter, the solutes have been nonelectrolytes that dissolve physically without dissociation or any other accompanying process. Each molecule that dissolves yields one dissolved solute molecule. The dissolution of an electroyte, however, is not this simple, as illustrated by the two common examples below:
Considering the first of these examples, and assuming complete dissociation, a 1.0 m aqueous solution of NaCl contains 2.0 mole of ions (1.0 mol Na+ and 1.0 mol Cl−) per each kilogram of water, and its freezing point depression is expected to be
When this solution is actually prepared and its freezing point depression measured, however, a value of 3.4 °C is obtained. Similar discrepancies are observed for other ionic compounds, and the differences between the measured and expected colligative property values typically become more significant as solute concentrations increase. These observations suggest that the ions of sodium chloride (and other strong electrolytes) are not completely dissociated in solution.
To account for this and avoid the errors accompanying the assumption of total dissociation, an experimentally measured parameter named in honor of Nobel Prize-winning German chemist Jacobus Henricus van’t Hoff is used. The van’t Hoff factor (i) is defined as the ratio of solute particles in solution to the number of formula units dissolved:
Values for measured van’t Hoff factors for several solutes, along with predicted values assuming complete dissociation, are shown in Table 3.1.
Table 3.15
Predicated and Measured van’t Hoff Factors for Several 0.050 m Aqueous Solutions
| Formula unit | Classification | Dissolution products | i (predicted) | i (measured) |
|---|
| C12H22O11 (glucose) | Nonelectrolyte | C12H22O11 | 1 | 1.0 |
| NaCl | Strong electrolyte | Na+, Cl− | 2 | 1.9 |
| HCl | Strong electrolyte (acid) | H3O+, Cl− | 2 | 1.9 |
| MgSO4 | Strong electrolyte | Mg2+, SO42−, | 2 | 1.3 |
| MgCl2 | Strong electrolyte | Mg2+, 2Cl− | 3 | 2.7 |
| FeCl3 | Strong electrolyte | Fe3+, 3Cl− | 4 | 3.4 |
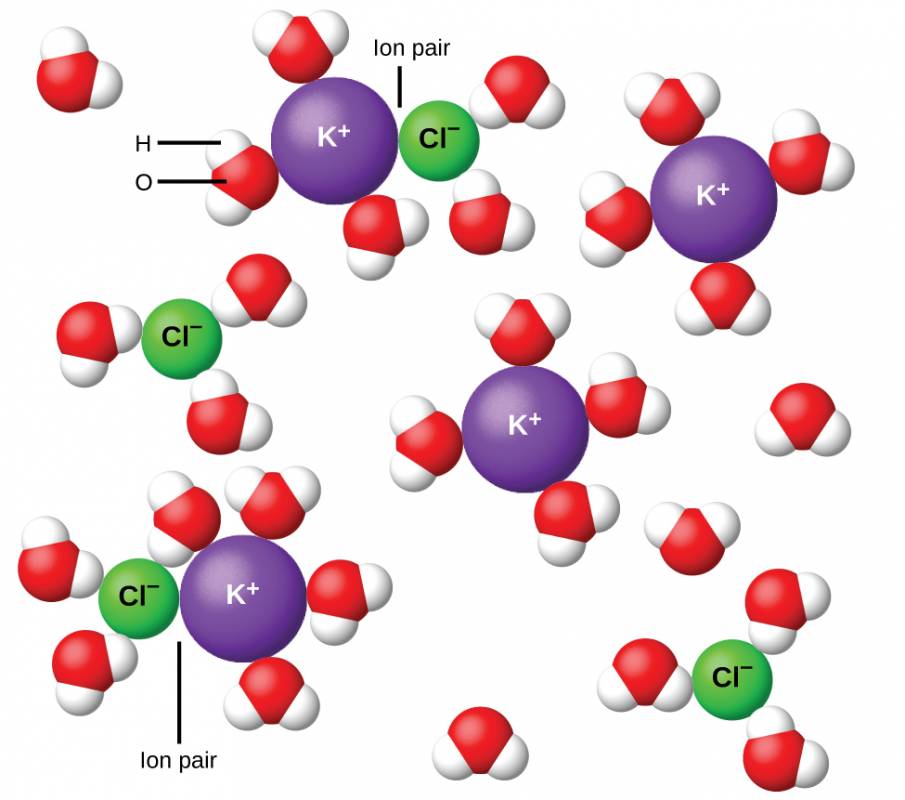
In 1923, the chemists Peter Debye and Erich Hückel proposed a theory to explain the apparent incomplete ionization of strong electrolytes. They suggested that although interionic attraction in an aqueous solution is very greatly reduced by solvation of the ions and the insulating action of the polar solvent, it is not completely nullified. The residual attractions prevent the ions from behaving as totally independent particles (Figure 3.15). In some cases, a positive and negative ion may actually touch, giving a solvated unit called an ion pair. Thus, the activity or the effective concentration of any particular kind of ion is less than that indicated by the actual concentration. Ions become more and more widely separated the more dilute the solution and the residual interionic attractions become less and less. Thus, in extremely dilute solutions, the effective concentrations of the ions (their activities) are essentially equal to the actual concentrations. Note that the van’t Hoff factors for the electrolytes in Table 3.1 are for 0.05 m solutions, at which concentration the value of i for NaCl is 1.9, as opposed to an ideal value of 2.
Figure 3.16
Dissociation of ionic compounds in water is not always complete due to the formation of ion pairs.