Decision-based learning (DBL) is a teaching method that organizes instruction around the conditional knowledge that guides experts’ decision-making processes. Briefly, conditional knowledge is knowing “when or under what conditions” to apply procedures and concepts (Bransford, Brown, Cocking, & Center, 2000). In short, DBL is organized around a functional sequence rather than a logical sequence.

For experts (which includes most instructors), their recognition of conditions has become so automatic as to seem intuitive. This phenomenon has become known as the "expert blind spot" (Cardenas, West, Swan, & Plummer, 2020). Consequently, this essential knowledge remains invisible to students in most forms of instruction. However, conditional knowledge is essential for successfully analyzing situations and selecting an appropriate course of action. Conditional knowledge is also a necessary foundation for well-developed conceptual understanding (Swan, Plummer, & West, 2020).

DBL seeks to reveal this conditional knowledge. Using a form of cognitive task analysis, an expert breaks down decisions they make based on the conditions in a real-world problem/artifact/scenario. This process serves to classify the problem and, therefore, signal a correct/appropriate/optimal action for the given situation.

The decision-making process can be structured as a series of questions (decisions) with possible responses. Decisions lead to a culminating action or resolution. The result is an expert decision model (EDM), which can be represented visually (Plummer, Swan, & Lush, 2017). An EDM may be linear, branching, or looping or may exhibit a combination of these patterns (for example, see Figure 1).

Figure 1

Portion of an Expert Decision Model (EDM) Used in a Basic Statistics Course

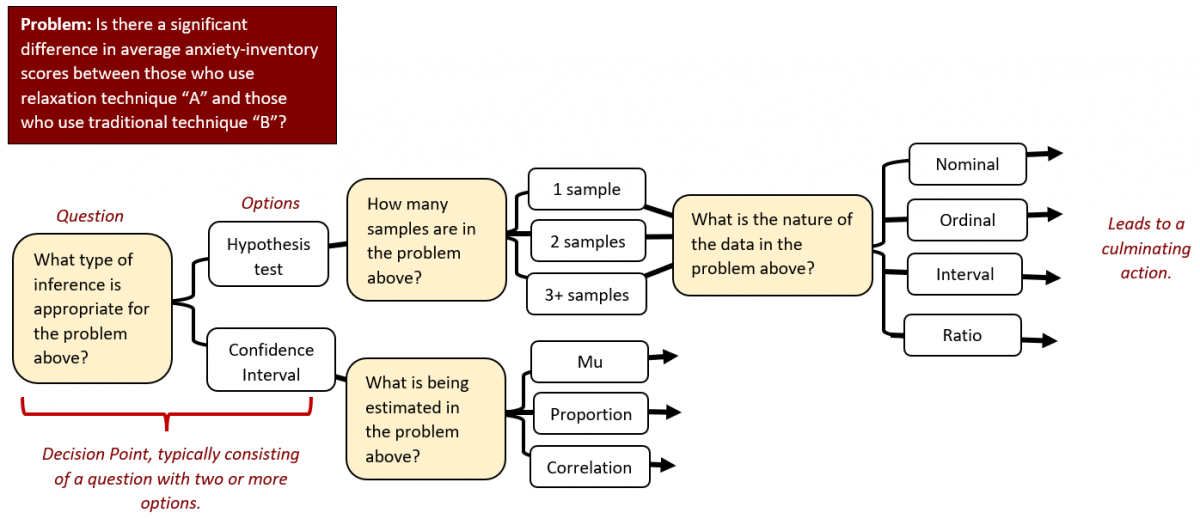
An EDM should focus on a single learning outcome (i.e., culminating action) and the object of analysis for that learning outcome (e.g., problem). For example, Plummer, Kebritchi, Leary, and Halverson (2022) describe several culminating actions as follows:

At the end of each decision path is a culminating action or decision. For example, in a chemistry course, the culminating action at the end of their decision model was to determine if the correct technique had been located to solve a heat and enthalpy problem (Sansom, Suh, & Plummer, 2019). In a qualitative inquiry course, the culminating action was to determine the credibility of a published qualitative study (Owens & Mills, 2021). Finally, in a mechanical engineering course, the culminating action was to determine the design and performance of a machine element (Nelson, 2021). (p. 5)

It should be noted that a given learning outcome, and therefore an EDM, includes a range of problem types. These problem types share many characteristics but also have defining characteristics that make them distinct. For example, heat and enthalpy are two high-level problem types which also contain problem types within themselves. The more closely related, the more characteristics they share until there may be only one distinguishing characteristic between a problem type and its nearest sibling(s).

Given a real-world problem or scenario, students navigate a series of stepwise decision points, learning how to reason through a scenario leading to an appropriate culminating action. Instruction occurs at each decision point focusing on how to identify the defining conditions in the given problem for the current decision. Instruction should be limited to what is essential to make that specific decision. We refer to this as just-enough, just-in-time instruction. The concise nature of this instruction helps students focus on and separate the defining condition for that decision from other sibling or cosmetic conditions in the scenario.

Initially, learners may have difficulty distinguishing cosmetic conditions from defining conditions. With sufficient repetition, learners develop the ability to distinguish defining conditions that lead to resolution of the problem. To provide sufficient repetition, a robust bank of multiple problems for each problem type is ideal. One way to quickly create problems is to keep the same cosmetic conditions and alter the defining conditions to account for each problem type.

Finally, DBL includes frequent, interleaved assessment without the aid of the EDM. Initially, instruction is highly scaffolded by the EDM and associated instruction. However, students tend to over-rely on the model unless they are required to perform without scaffolding. Frequent, low-stakes assessments that require equal performance without the model are essential to prompt students to internalize their learning. In this way, students begin to develop a functional schema of the domain.

With practice, DBL helps students begin to conceptualize individual real-world situations as instances of a problem type. In other words, they begin to generate a functional schema allowing them to independently apply their learning in real-world situations. Further, with conditional knowledge as the organizing principle, students have an opportunity to see how conditions have patterns that invoke relevant concepts and procedures. As they delve deeper, this framework also helps students understand the boundaries and application of underlying theories, principles, and concepts of the domain.

References

Bransford, J., Brown, A., Cocking, R., & Center, E. R. I. (2000). How People Learn: Brain, Mind, Experience, and School 2nd ed.). Washington, D.C.: National Academy Press.

Cardenas, C., West, R. E., Swan, R. H., & Plummer, K. J. (2020). Modeling Expertise through Decision-based Learning: Theory, Practice, and Technology Applications. Revista de Educación a Distancia (RED), 20(64). doi:10.6018/red.408651

Nelson, T. G. (2021). Exploring Decision-Based Learning in an Engineering Context. In N. Wentworth, K. J. Plummer, & R. H. Swan (Eds.), Decision-Based Learning: An Innovative Pedagogy that Unpacks Expert Knowledge for the Novice Learner (pp. 55-65): Emerald Publishing Limited.

Owens, M. A., & Mills, E. R. (2021). Using Decision-Based Learning to Teach Qualitative Research Evaluation. In N. Wentworth, K. J. Plummer, & R. H. Swan (Eds.), Decision-Based Learning: An Innovative Pedagogy that Unpacks Expert Knowledge for the Novice Learner (pp. 93-102): Emerald Publishing Limited.

Plummer, K. J., Kebritchi, M., Leary, H. M., & Halverson, D. M. (2022). Enhancing Critical Thinking Skills through Decision-Based Learning. Innovative Higher Education, 47(4), 711-734. doi:10.1007/s10755-022-09595-9

Plummer, K. J., Swan, R. H., & Lush, N. (2017). Introduction to Decision-Based Learning. Paper presented at the 11th International Technology, Education and Development Conference, Valencia, Spain.

Sansom, R. L., Suh, E., & Plummer, K. J. (2019). Decision-Based Learning: ″If I Just Knew Which Equation To Use, I Know I Could Solve This Problem!″. Journal of Chemical Education, 96(3), 445-454. doi:10.1021/acs.jchemed.8b00754

Swan, R. H., Plummer, K. J., & West, R. E. (2020). Toward functional expertise through formal education: Identifying an opportunity for higher education. Educational Technology Research & Development, 68(5), 2551-2568. doi:10.1007/s11423-020-09778-1