Radioactive Decay

An atomic nucleus consists of protons and neutrons, collectively called nucleons. Although protons repel each other, the nucleus is held tightly together by a short-range, but very strong, force called the strong nuclear force. Of the many nuclides that exist, only a small number are stable. Nuclides with even numbers of protons or neutrons, or those with magic numbers of nucleons, are especially likely to be stable. These stable nuclides occupy a narrow band of stability on a graph of number of protons versus number of neutrons. Nuclei can undergo reactions that change their number of protons, number of neutrons, or energy state. Many different particles can be involved in nuclear reactions. The most common are protons, neutrons, positrons (which are positively charged electrons), alpha (α) particles (which are high-energy helium nuclei), beta (β) particles (which are high-energy electrons), and gamma (γ) rays (which compose high-energy electromagnetic radiation). As with chemical reactions, nuclear reactions are always balanced. When a nuclear reaction occurs, the total mass (number) and the total charge remain unchanged. Nuclei that have unstable n:p ratios undergo spontaneous radioactive decay. The most common types of radioactivity are α decay, β decay, γ emission, positron emission, and electron capture. Nuclear reactions also often involve γ rays, and some nuclei decay by electron capture. Each of these modes of decay leads to the formation of a new nucleus with a more stable n:p ratio. Some substances undergo radioactive decay series, proceeding through multiple decays before ending in a stable isotope.

11.1 Structure and Stability

Learning Objectives

By the end of this section, you will be able to:

Describe nuclear structure in terms of protons, neutrons, and electrons
Explain trends in the relative stability of nuclei

Nuclear chemistry is the study of reactions that involve changes in nuclear structure. The chapter on atoms, molecules, and ions introduced the basic idea of nuclear structure, that the nucleus of an atom is composed of protons and, with the exception of $_{1}^{1} H,$ neutrons. Recall that the number of protons in the nucleus is called the atomic number (Z) of the element, and the sum of the number of protons and the number of neutrons is the mass number (A). Atoms with the same atomic number but different mass numbers are isotopes of the same element. When referring to a single type of nucleus, we often use the term nuclide and identify it by the notation $_{Z}^{A} X,$ where X is the symbol for the element, A is the mass number, and Z is the atomic number (for example, $_{6}^{14} C) .$ Often a nuclide is referenced by the name of the element followed by a hyphen and the mass number. For example, $_{6}^{14} C$ is called “carbon-14.”

Protons and neutrons, collectively called nucleons, are packed together tightly in a nucleus. With a radius of about 10⁻¹⁵ meters, a nucleus is quite small compared to the radius of the entire atom, which is about 10⁻¹⁰ meters. Nuclei are extremely dense compared to bulk matter, averaging 1.8 $\times$ 10¹⁴ grams per cubic centimeter. For example, water has a density of 1 gram per cubic centimeter, and iridium, one of the densest elements known, has a density of 22.6 g/cm³. If the earth’s density were equal to the average nuclear density, the earth’s radius would be only about 200 meters (earth’s actual radius is approximately 6.4 $\times$ 10⁶ meters, 30,000 times larger). Example 11.1 demonstrates just how great nuclear densities can be in the natural world.

EXAMPLE 11.1

Density of a Neutron Star

Neutron stars form when the core of a very massive star undergoes gravitational collapse, causing the star’s outer layers to explode in a supernova. Composed almost completely of neutrons, they are the densest-known stars in the universe, with densities comparable to the average density of an atomic nucleus. A neutron star in a faraway galaxy has a mass equal to 2.4 solar masses (1 solar mass =

M_{☉}

= mass of the sun = 1.99

\times

10³⁰ kg) and a diameter of 26 km.

(a) What is the density of this neutron star?

(b) How does this neutron star’s density compare to the density of a uranium nucleus, which has a diameter of about 15 fm (1 fm = 10^–15 m)?

Solution

We can treat both the neutron star and the U-235 nucleus as spheres. Then the density for both is given by:

d = \frac{m}{V} with V = \frac{4}{3} π r^{3}

(a) The radius of the neutron star is $\frac{1}{2} \times 26 km = \frac{1}{2} \times 2.6 \times 10^{4} m = 1.3 \times 10^{4} m,$ so the density of the neutron star is:

d = \frac{m}{V} = \frac{m}{\frac{4}{3} π r^{3}} = \frac{2.4 (1.99 \times 10^{30} kg)}{\frac{4}{3} π {(1.3 \times 10^{4} m)}^{3}} = 5.2 \times 10^{17} {kg/m}^{3}

(b) The radius of the U-235 nucleus is $\frac{1}{2} \times 15 \times 10^{−15} m = 7.5 \times 10^{−15} m,$ so the density of the U-235 nucleus is:

d = \frac{m}{V} = \frac{m}{\frac{4}{3} π r^{3}} = \frac{235 amu (\frac{1.66 \times 10^{−27} kg}{1 amu})}{\frac{4}{3} π {(7.5 \times 10^{−15} m)}^{3}} = 2.2 \times 10^{17} {kg/m}^{3}

These values are fairly similar (same order of magnitude), but the neutron star is more than twice as dense as the U-235 nucleus.

Check Your Learning

Find the density of a neutron star with a mass of 1.97 solar masses and a diameter of 13 km, and compare it to the density of a hydrogen nucleus, which has a diameter of 1.75 fm (1 fm = 1

\times

10^–15 m).

Answer

The density of the neutron star is 3.4 $\times$ 10¹⁸ kg/m³. The density of a hydrogen nucleus is 6.0 $\times$ 10¹⁷ kg/m³. The neutron star is 5.7 times denser than the hydrogen nucleus.

To hold positively charged protons together in the very small volume of a nucleus requires very strong attractive forces because the positively charged protons repel one another strongly at such short distances. The force of attraction that holds the nucleus together is the strong nuclear force. (The strong force is one of the four fundamental forces that are known to exist. The others are the electromagnetic force, the gravitational force, and the nuclear weak force.) This force acts between protons, between neutrons, and between protons and neutrons. It is very different from the electrostatic force that holds negatively charged electrons around a positively charged nucleus (the attraction between opposite charges). Over distances less than 10⁻¹⁵ meters and within the nucleus, the strong nuclear force is much stronger than electrostatic repulsions between protons; over larger distances and outside the nucleus, it is essentially nonexistent.

LINK TO LEARNING

Visit this website for more information about the four fundamental forces.

11.1.2 Nuclear Stability

A nucleus is stable if it cannot be transformed into another configuration without adding energy from the outside. Of the thousands of nuclides that exist, about 250 are stable. A plot of the number of neutrons versus the number of protons for stable nuclei reveals that the stable isotopes fall into a narrow band. This region is known as the band of stability (also called the belt, zone, or valley of stability). The straight line in Figure 11.1 represents nuclei that have a 1:1 ratio of protons to neutrons (n:p ratio). Note that the lighter stable nuclei, in general, have equal numbers of protons and neutrons. For example, nitrogen-14 has seven protons and seven neutrons. Heavier stable nuclei, however, have increasingly more neutrons than protons. For example: iron-56 has 30 neutrons and 26 protons, an n:p ratio of 1.15, whereas the stable nuclide lead-207 has 125 neutrons and 82 protons, an n:p ratio equal to 1.52. This is because larger nuclei have more proton-proton repulsions, and require larger numbers of neutrons to provide compensating strong forces to overcome these electrostatic repulsions and hold the nucleus together.

Figure 11.1

This plot shows the nuclides that are known to exist and those that are stable. The stable nuclides are indicated in blue, and the unstable nuclides are indicated in green. Note that all isotopes of elements with atomic numbers greater than 83 are unstable. The solid line is the line where n = Z.

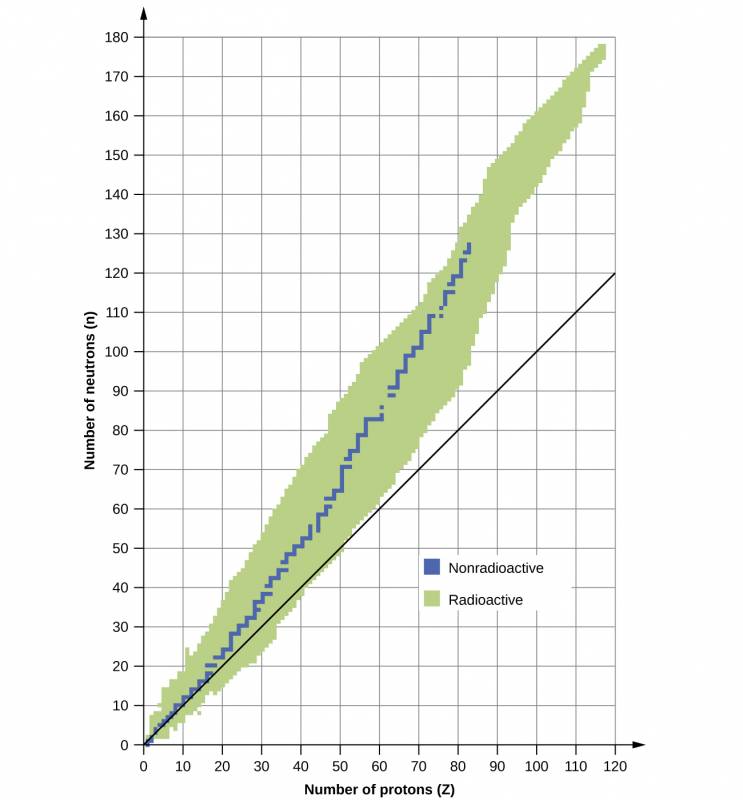
A graph is shown where the x-axis is labeled “Number of neutrons, open parenthesis, n, close parenthesis” and has values of 0 to 180 in increments of 10. The y-axis is labeled “Number of protons, open parenthesis, Z, close parenthesis” and has values of 0 to 120 in increments of 10. A green shaded band of varying width, labeled “Radioactive,” extends from point 0 on both axes to 178 on the y-axis and 118 on the x-axis in a linear manner. The width of this band varies from 8 to 18 units in width according to the x-axis measurements. A blue line in a roughly zig-zag pattern runs through the middle of the shaded band and stops at 128 on the y-axis and 82 on the x-axis. This line is labeled “Nonradioactive.” An unlabeled, black, solid line extends from point 0, 0 to 120, 120 in a linear manner.

The nuclei that are to the left or to the right of the band of stability are unstable and exhibit radioactivity. They change spontaneously (decay) into other nuclei that are either in, or closer to, the band of stability. These nuclear decay reactions convert one unstable isotope (or radioisotope) into another, more stable, isotope. We will discuss the nature and products of this radioactive decay in subsequent sections of this chapter.

Several observations may be made regarding the relationship between the stability of a nucleus and its structure. Nuclei with even numbers of protons, neutrons, or both are more likely to be stable (see Table 11.1). Nuclei with certain numbers of nucleons, known as magic numbers, are stable against nuclear decay. These numbers of protons or neutrons (2, 8, 20, 28, 50, 82, and 126) make complete shells in the nucleus. These are similar in concept to the stable electron shells observed for the noble gases. Nuclei that have magic numbers of both protons and neutrons, such as $_{2}^{4} He,$ $_{8}^{16} O,$ $_{20}^{40} Ca,$ and $_{82}^{208} Pb,$ are called “double magic” and are particularly stable. These trends in nuclear stability may be rationalized by considering a quantum mechanical model of nuclear energy states analogous to that used to describe electronic states earlier in this textbook. The details of this model are beyond the scope of this chapter.

Table 11.2

Stable Nuclear Isotopes

Number of Stable Isotopes	Proton Number	Neutron Number
157	even	even
53	even	odd
50	odd	even
5	odd	odd

11.2 Nuclear Equations

Learning Objectives

By the end of this section, you will be able to:

Identify common particles and energies involved in nuclear reactions
Write and balance nuclear equations

Changes of nuclei that result in changes in their atomic numbers, mass numbers, or energy states are nuclear reactions. To describe a nuclear reaction, we use an equation that identifies the nuclides involved in the reaction, their mass numbers and atomic numbers, and the other particles involved in the reaction.

11.2.1 Types of Particles in Nuclear Reactions

Many entities can be involved in nuclear reactions. The most common are protons, neutrons, alpha particles, beta particles, positrons, and gamma rays, as shown in Figure 11.2. Protons $(_{1}^{1} p,$ also represented by the symbol $_{1}^{1} H)$ and neutrons $(_{0}^{1} n)$ are the constituents of atomic nuclei, and have been described previously. Alpha particles $(_{2}^{4} He,$ also represented by the symbol $_{2}^{4} α)$ are high-energy helium nuclei. Beta particles $(_{−1}^{0} β,$ also represented by the symbol $_{−1}^{0} e)$ are high-energy electrons, and gamma rays are photons of very high-energy electromagnetic radiation. Positrons $(_{+1}^{0} e,$ also represented by the symbol $_{+1}^{0} β)$ are positively charged electrons (“anti-electrons”). The subscripts and superscripts are necessary for balancing nuclear equations, but are usually optional in other circumstances. For example, an alpha particle is a helium nucleus (He) with a charge of +2 and a mass number of 4, so it is symbolized $_{2}^{4} He .$ This works because, in general, the ion charge is not important in the balancing of nuclear equations.

Figure 11.3

Although many species are encountered in nuclear reactions, this table summarizes the names, symbols, representations, and descriptions of the most common of these.

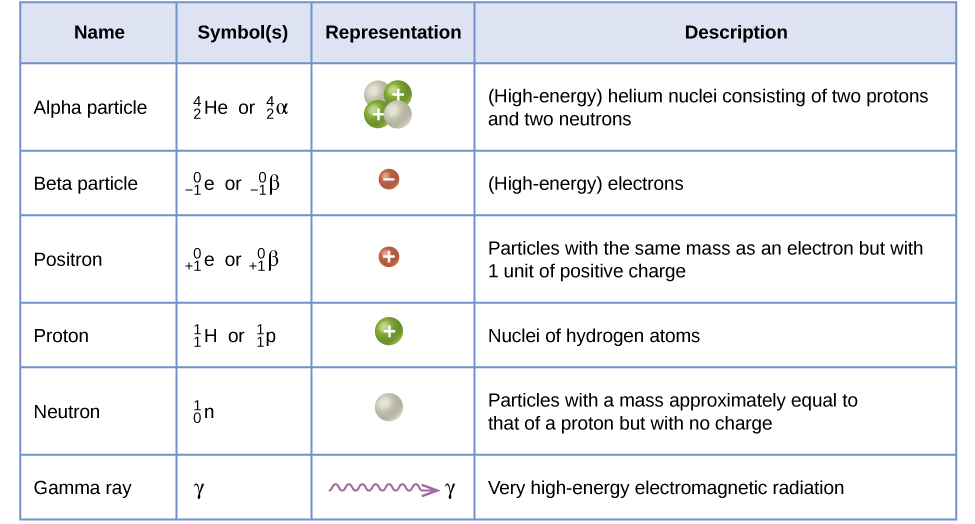
This table has four columns and seven rows. The first row is a header row and it labels each column: “Name,” “Symbol(s),” “Representation,” and “Description.” Under the “Name” column are the following: “Alpha particle,” “Beta particle,” “Positron,” “Proton,” “Neutron,” and “Gamma ray.” Under the “Symbol(s)” column are the following: “ superscript 4 stacked over a subscript 2 H e or lowercase alpha,” “superscript 0 stacked over a subscript 1 e or lowercase beta,” “superscript 0 stacked over a positive subscript 1 e or lowercase beta superscript positive sign,” “superscript 1 stacked over a subscript 1 H or lowercase rho superscript 1 stacked over a subscript 1 H,” “superscript 1 stacked over a subscript 0 n or lowercase eta superscript 1 stacked over a subscript 0 n,” and a lowercase gamma. Under the “Representation column,” are the following: two white sphere attached to two blue spheres of about the same size with positive signs in them; a small red sphere with a negative sign in it; a small red sphere with a positive sign in it; a blue spheres with a positive sign in it; a white sphere; and a purple squiggle ling with an arrow pointing right to a lowercase gamma. Under the “Description” column are the following: “(High-energy) helium nuclei consisting of two protons and two neutrons,” “(High-energy) elections,” “Particles with the same mass as an electron but with 1 unit of positive charge,” “Nuclei of hydrogen atoms,” “Particles with a mass approximately equal to that of a proton but with no charge,” and “Very high-energy electromagnetic radiation.”

Note that positrons are exactly like electrons, except they have the opposite charge. They are the most common example of antimatter, particles with the same mass but the opposite state of another property (for example, charge) than ordinary matter. When antimatter encounters ordinary matter, both are annihilated and their mass is converted into energy in the form of gamma rays (γ)—and other much smaller subnuclear particles, which are beyond the scope of this chapter—according to the mass-energy equivalence equation E = mc², seen in the preceding section. For example, when a positron and an electron collide, both are annihilated and two gamma ray photons are created:

_{−1}^{0} e +_{+1}^{0} e ⟶ γ + γ

As seen in the chapter discussing light and electromagnetic radiation, gamma rays compose short wavelength, high-energy electromagnetic radiation and are (much) more energetic than better-known X-rays that can behave as particles in the wave-particle duality sense. Gamma rays are a type of high energy electromagnetic radiation produced when a nucleus undergoes a transition from a higher to a lower energy state, similar to how a photon is produced by an electronic transition from a higher to a lower energy level. Due to the much larger energy differences between nuclear energy shells, gamma rays emanating from a nucleus have energies that are typically millions of times larger than electromagnetic radiation emanating from electronic transitions.

11.2.2 Balancing Nuclear Reactions

A balanced chemical reaction equation reflects the fact that during a chemical reaction, bonds break and form, and atoms are rearranged, but the total numbers of atoms of each element are conserved and do not change. A balanced nuclear reaction equation indicates that there is a rearrangement during a nuclear reaction, but of nucleons (subatomic particles within the atoms’ nuclei) rather than atoms. Nuclear reactions also follow conservation laws, and they are balanced in two ways:

The sum of the mass numbers of the reactants equals the sum of the mass numbers of the products.
The sum of the charges of the reactants equals the sum of the charges of the products.

If the atomic number and the mass number of all but one of the particles in a nuclear reaction are known, we can identify the particle by balancing the reaction. For instance, we could determine that $_{8}^{17} O$ is a product of the nuclear reaction of $_{7}^{14} N$ and $_{2}^{4} He$ if we knew that a proton, $_{1}^{1} H,$ was one of the two products. Example 11.2 shows how we can identify a nuclide by balancing the nuclear reaction.

EXAMPLE 11.2.3

Balancing Equations for Nuclear Reactions

The reaction of an α particle with magnesium-25

(_{12}^{25} Mg)

produces a proton and a nuclide of another element. Identify the new nuclide produced.

Solution

The nuclear reaction can be written as:

_{12}^{25} Mg +_{2}^{4} He ⟶_{1}^{1} H +_{Z}^{A} X

where A is the mass number and Z is the atomic number of the new nuclide, X. Because the sum of the mass numbers of the reactants must equal the sum of the mass numbers of the products:

25 + 4 = A + 1, or A = 28

Similarly, the charges must balance, so:

12 + 2 = Z + 1, and Z = 13

Check the periodic table: The element with nuclear charge = +13 is aluminum. Thus, the product is $_{13}^{28} Al .$

Check Your Learning

The nuclide

_{53}^{125} I

combines with an electron and produces a new nucleus and no other massive particles. What is the equation for this reaction?

Answer

$_{53}^{125} I +_{−1}^{0} e ⟶_{52}^{125} Te$

Following are the equations of several nuclear reactions that have important roles in the history of nuclear chemistry:

The first naturally occurring unstable element that was isolated, polonium, was discovered by the Polish scientist Marie Curie and her husband Pierre in 1898. It decays, emitting α particles:
$_{84}^{212} Po ⟶_{82}^{208} Pb +_{2}^{4} He$
The first nuclide to be prepared by artificial means was an isotope of oxygen, ¹⁷O. It was made by Ernest Rutherford in 1919 by bombarding nitrogen atoms with α particles:
$_{7}^{14} N +_{2}^{4} He ⟶_{8}^{17} O +_{1}^{1} H$
James Chadwick discovered the neutron in 1932, as a previously unknown neutral particle produced along with ¹²C by the nuclear reaction between ⁹Be and ⁴He:
$_{4}^{9} Be +_{2}^{4} He ⟶_{6}^{12} C +_{0}^{1} n$
The first element to be prepared that does not occur naturally on the earth, technetium, was created by bombardment of molybdenum by deuterons (heavy hydrogen, $_{1}^{2} H)$ , by Emilio Segre and Carlo Perrier in 1937:
$_{1}^{2} H +_{42}^{97} Mo ⟶ 2_{0}^{1} n +_{43}^{97} Tc$
The first controlled nuclear chain reaction was carried out in a reactor at the University of Chicago in 1942. One of the many reactions involved was:
$_{92}^{235} U +_{0}^{1} n ⟶_{35}^{87} Br +_{57}^{146} La + 3_{0}^{1} n$

11.3 Radioactive Decay

Learning Objectives

By the end of this section, you will be able to:

Recognize common modes of radioactive decay
Identify common particles and energies involved in nuclear decay reactions
Write and balance nuclear decay equations

Following the somewhat serendipitous discovery of radioactivity by Becquerel, many prominent scientists began to investigate this new, intriguing phenomenon. Among them were Marie Curie (the first woman to win a Nobel Prize, and the only person to win two Nobel Prizes in different sciences—chemistry and physics), who was the first to coin the term “radioactivity,” and Ernest Rutherford (of gold foil experiment fame), who investigated and named three of the most common types of radiation. During the beginning of the twentieth century, many radioactive substances were discovered, the properties of radiation were investigated and quantified, and a solid understanding of radiation and nuclear decay was developed.

The spontaneous change of an unstable nuclide into another is radioactive decay. The unstable nuclide is called the parent nuclide; the nuclide that results from the decay is known as the daughter nuclide. The daughter nuclide may be stable, or it may decay itself. The radiation produced during radioactive decay is such that the daughter nuclide lies closer to the band of stability than the parent nuclide, so the location of a nuclide relative to the band of stability can serve as a guide to the kind of decay it will undergo (Figure 11.3).

Figure 11.4

A nucleus of uranium-238 (the parent nuclide) undergoes α decay to form thorium-234 (the daughter nuclide). The alpha particle removes two protons (green) and two neutrons (gray) from the uranium-238 nucleus.

A diagram shows two spheres composed of many smaller white and green spheres connected by a right-facing arrow with another, down-facing arrow coming off of it. The left sphere, labeled “Parent nucleus uranium dash 238” has two white and two green spheres that are near one another and are outlined in red. These two green and two white spheres are shown near the tip of the down-facing arrow and labeled “alpha particle.” The right sphere, labeled “Daughter nucleus radon dash 234,” looks the same as the left, but has a space for four smaller spheres outlined with a red dotted line.

LINK TO LEARNING

Although the radioactive decay of a nucleus is too small to see with the naked eye, we can indirectly view radioactive decay in an environment called a cloud chamber. Click here to learn about cloud chambers and to view an interesting Cloud Chamber Demonstration from the Jefferson Lab.

11.3.1 Types of Radioactive Decay

Ernest Rutherford’s experiments involving the interaction of radiation with a magnetic or electric field (Figure 11.4) helped him determine that one type of radiation consisted of positively charged and relatively massive α particles; a second type was made up of negatively charged and much less massive β particles; and a third was uncharged electromagnetic waves, γ rays. We now know that α particles are high-energy helium nuclei, β particles are high-energy electrons, and γ radiation compose high-energy electromagnetic radiation. We classify different types of radioactive decay by the radiation produced.

Figure 11.5

Alpha particles, which are attracted to the negative plate and deflected by a relatively small amount, must be positively charged and relatively massive. Beta particles, which are attracted to the positive plate and deflected a relatively large amount, must be negatively charged and relatively light. Gamma rays, which are unaffected by the electric field, must be uncharged.

A diagram is shown. A gray box on the left side of the diagram labeled “Lead block” has a chamber hollowed out in the center in which a sample labeled “Radioactive substance” is placed. A blue beam is coming from the sample, out of the block, and passing through two horizontally placed plates that are labeled “Electrically charged plates.” The top plate is labeled with a positive sign while the bottom plate is labeled with a negative sign. The beam is shown to break into three beams as it passes in between the plates; in order from top to bottom, they are red, labeled “beta rays,” purple labeled “gamma rays” and green labeled “alpha rays.” The beams are shown to hit a vertical plate labeled “Photographic plate” on the far right side of the diagram.

Alpha (α) decay is the emission of an α particle from the nucleus. For example, polonium-210 undergoes α decay:

_{84}^{210} Po ⟶_{2}^{4} He +_{82}^{206} Pb or_{84}^{210} Po ⟶_{2}^{4} α +_{82}^{206} Pb

Alpha decay occurs primarily in heavy nuclei (A > 200, Z > 83). Because the loss of an α particle gives a daughter nuclide with a mass number four units smaller and an atomic number two units smaller than those of the parent nuclide, the daughter nuclide has a larger n:p ratio than the parent nuclide. If the parent nuclide undergoing α decay lies below the band of stability (refer to Figure 11.1), the daughter nuclide will lie closer to the band.

Beta (β) decay is the emission of an electron from a nucleus. Iodine-131 is an example of a nuclide that undergoes β decay:

_{53}^{131} I ⟶_{-1}^{0} e +_{54}^{131} Xe or_{53}^{131} I ⟶_{-1}^{0} β +_{54}^{131} Xe

Beta decay, which can be thought of as the conversion of a neutron into a proton and a β particle, is observed in nuclides with a large n:p ratio. The beta particle (electron) emitted is from the atomic nucleus and is not one of the electrons surrounding the nucleus. Such nuclei lie above the band of stability. Emission of an electron does not change the mass number of the nuclide but does increase the number of its protons and decrease the number of its neutrons. Consequently, the n:p ratio is decreased, and the daughter nuclide lies closer to the band of stability than did the parent nuclide.

Gamma emission (γ emission) is observed when a nuclide is formed in an excited state and then decays to its ground state with the emission of a γ ray, a quantum of high-energy electromagnetic radiation. The presence of a nucleus in an excited state is often indicated by an asterisk (*). Cobalt-60 emits γ radiation and is used in many applications including cancer treatment:

_{27}^{60} Co* ⟶_{0}^{0} γ +_{27}^{60} Co

There is no change in mass number or atomic number during the emission of a γ ray unless the γ emission accompanies one of the other modes of decay.

Positron emission (β⁺ decay) is the emission of a positron from the nucleus. Oxygen-15 is an example of a nuclide that undergoes positron emission:

_{8}^{15} O ⟶_{+1}^{0} e +_{7}^{15} N or_{8}^{15} O ⟶_{+1}^{0} β +_{7}^{15} N

Positron emission is observed for nuclides in which the n:p ratio is low. These nuclides lie below the band of stability. Positron decay is the conversion of a proton into a neutron with the emission of a positron. The n:p ratio increases, and the daughter nuclide lies closer to the band of stability than did the parent nuclide.

Electron capture occurs when one of the inner electrons in an atom is captured by the atom’s nucleus. For example, potassium-40 undergoes electron capture:

_{19}^{40} K +_{-1}^{0} e ⟶_{18}^{40} Ar

Electron capture occurs when an inner shell electron combines with a proton and is converted into a neutron. The loss of an inner shell electron leaves a vacancy that will be filled by one of the outer electrons. As the outer electron drops into the vacancy, it will emit energy. In most cases, the energy emitted will be in the form of an X-ray. Like positron emission, electron capture occurs for “proton-rich” nuclei that lie below the band of stability. Electron capture has the same effect on the nucleus as does positron emission: The atomic number is decreased by one and the mass number does not change. This increases the n:p ratio, and the daughter nuclide lies closer to the band of stability than did the parent nuclide. Whether electron capture or positron emission occurs is difficult to predict. The choice is primarily due to kinetic factors, with the one requiring the smaller activation energy being the one more likely to occur.

Figure 11.5 summarizes these types of decay, along with their equations and changes in atomic and mass numbers.

Figure 11.6

This table summarizes the type, nuclear equation, representation, and any changes in the mass or atomic numbers for various types of decay.

This table has four columns and six rows. The first row is a header row and it labels each column: “Type,” “Nuclear equation,” “Representation,” and “Change in mass / atomic numbers.” Under the “Type” column are the following: “Alpha decay,” “Beta decay,” “Gamma decay,” “Positron emission,” and “Electron capture.” Under the “Nuclear equation” column are several equations. Each begins with superscript A stacked over subscript Z X. There is a large gap of space and then the following equations: “superscript 4 stacked over subscript 2 He plus superscript A minus 4 stacked over subscript Z minus 2 Y,” “superscript 0 stacked over subscript negative 1 e plus superscript A stacked over subscript Z plus 1 Y,” “superscript 0 stacked over subscript 0 lowercase gamma plus superscript A stacked over subscript Z Y,” “superscript 0 stacked over subscript positive 1 e plus superscript A stacked over subscript Y minus 1 Y,” and “superscript 0 stacked over subscript negative 1 e plus superscript A stacked over subscript Y minus 1 Y.” Under the “Representation” column are the five diagrams. The first shows a cluster of green and white spheres. A section of the cluster containing two white and two green spheres is outlined. There is a right-facing arrow pointing to a similar cluster as previously described, but the outlined section is missing. From the arrow another arrow branches off and points downward. The small cluster to two white spheres and two green spheres appear at the end of the arrow. The next diagram shows the same cluster of white and green spheres. One white sphere is outlined. There is a right-facing arrow to a similar cluster, but the white sphere is missing. Another arrow branches off the main arrow and a red sphere with a negative sign appears at the end. The next diagram shows the same cluster of white and green spheres. The whole sphere is outlined and labeled, “excited nuclear state.” There is a right-facing arrow that points to the same cluster. No spheres are missing. Off the main arrow is another arrow which points to a purple squiggle arrow which in turn points to a lowercase gamma. The next diagram shows the same cluster of white and green spheres. One green sphere is outlined. There is a right-facing arrow to a similar cluster, but the green sphere is missing. Another arrow branches off the main arrow and a red sphere with a positive sign appears at the end. The next diagram shows the same cluster of white and green spheres. One green sphere is outlined. There is a right-facing arrow to a similar cluster, but the green sphere is missing. Two other arrows branch off the main arrow. The first shows a gold sphere with a negative sign joining with the right-facing arrow. The secon points to a blue squiggle arrow labeled, “X-ray.” Under the “Change in mass / atomic numbers” column are the following: “A: decrease by 4, Z: decrease by 2,” “A: unchanged, Z: increased by 1,” “A: unchanged, Z: unchanged,” “A: unchanged, Z: unchanged,” “A: unchanged, Z: decrease by 1,” and “A: unchanged, Z: decrease by 1.”

11.3.2 CHEMISTRY IN EVERYDAY LIFE

PET Scan

Positron emission tomography (PET) scans use radiation to diagnose and track health conditions and monitor medical treatments by revealing how parts of a patient’s body function (Figure 11.6). To perform a PET scan, a positron-emitting radioisotope is produced in a cyclotron and then attached to a substance that is used by the part of the body being investigated. This “tagged” compound, or radiotracer, is then put into the patient (injected via IV or breathed in as a gas), and how it is used by the tissue reveals how that organ or other area of the body functions.

Figure 12.7

A PET scanner (a) uses radiation to provide an image of how part of a patient’s body functions. The scans it produces can be used to image a healthy brain (b) or can be used for diagnosing medical conditions such as Alzheimer’s disease (c). (credit a: modification of work by Jens Maus)

Three pictures are shown and labeled “a,” “b” and “c.” Picture a shows a machine with a round opening connected to an examination table. Picture b is a medical scan of the top of a person’s head and shows large patches of yellow and red and smaller patches of blue, green and purple highlighting. Picture c also shows a medical scan of the top of a person’s head, but this image is mostly colored in blue and purple with very small patches of red and yellow.

For example, F-18 is produced by proton bombardment of ¹⁸O $(_{8}^{18} O +_{1}^{1} p ⟶_{9}^{18} F +_{0}^{1} n)$ and incorporated into a glucose analog called fludeoxyglucose (FDG). How FDG is used by the body provides critical diagnostic information; for example, since cancers use glucose differently than normal tissues, FDG can reveal cancers. The ¹⁸F emits positrons that interact with nearby electrons, producing a burst of gamma radiation. This energy is detected by the scanner and converted into a detailed, three-dimensional, color image that shows how that part of the patient’s body functions. Different levels of gamma radiation produce different amounts of brightness and colors in the image, which can then be interpreted by a radiologist to reveal what is going on. PET scans can detect heart damage and heart disease, help diagnose Alzheimer’s disease, indicate the part of a brain that is affected by epilepsy, reveal cancer, show what stage it is, and how much it has spread, and whether treatments are effective. Unlike magnetic resonance imaging and X-rays, which only show how something looks, the big advantage of PET scans is that they show how something functions. PET scans are now usually performed in conjunction with a computed tomography scan.

11.3.3 Radioactive Decay Series

The naturally occurring radioactive isotopes of the heaviest elements fall into chains of successive disintegrations, or decays, and all the species in one chain constitute a radioactive family, or radioactive decay series. Three of these series include most of the naturally radioactive elements of the periodic table. They are the uranium series, the actinide series, and the thorium series. The neptunium series is a fourth series, which is no longer significant on the earth because of the short half-lives of the species involved. Each series is characterized by a parent (first member) that has a long half-life and a series of daughter nuclides that ultimately lead to a stable end-product—that is, a nuclide on the band of stability (Figure 11.7). In all three series, the end-product is a stable isotope of lead. The neptunium series, previously thought to terminate with bismuth-209, terminates with thallium-205.

Figure 12.8

Uranium-238 undergoes a radioactive decay series consisting of 14 separate steps before producing stable lead-206. This series consists of eight α decays and six β decays.

A graph is shown where the x-axis is labeled “Number of neutrons, open parenthesis, n, close parenthesis” and has values of 122 to 148 in increments of 2. The y-axis is labeled “Atomic number” and has values of 80 to 92 in increments of 1. Two types of arrows are used in this graph to connect the points. Green arrows are labeled as “alpha decay” while red arrows are labeled “beta decay.” Beginning at the point “92, 146” that is labeled “superscript 238, U,” a green arrow connects this point to the second point “90, 144” which is labeled “superscript 234, T h.” A red arrow connect this to the third point “91, 143” which is labeled “superscript 234, P a” which is connected to the fourth point “92, 142” by a red arrow and which is labeled “superscript 234, U.” A green arrow leads to the next point, “90, 140” which is labeled “superscript 230, T h” and is connected by a green arrow to the sixth point, “88, 138” which is labeled “superscript 226, R a” that is in turn connected by a green arrow to the seventh point “86, 136” which is labeled “superscript 222, Ra.” The eighth point, at “84, 134” is labeled “superscript 218, P o” and has green arrows leading to it and away from it to the ninth point “82, 132” which is labeled “superscript 214, Pb” which is connected by a red arrow to the tenth point, “83, 131” which is labeled “superscript 214, B i.” A red arrow leads to the eleventh point “84, 130” which is labeled “superscript 214, P o” and a green arrow leads to the twelvth point “82, 128” which is labeled “superscript 210, P b.” A red arrow leads to the thirteenth point “83, 127” which is labeled “superscript 210, B i” and a red arrow leads to the fourteenth point “84, 126” which is labeled “superscript 210, P o.” The final point is labeled “82, 124” and “superscript 206, P b.”

Example: 11.3.4 Radioactive Decay

Previous Citation(s)

Flowers, P., et al. (2019). Chemistry: Atoms First 2e. https://openstax.org/details/books/chemistry-atoms-first-2e (20.1-20.3)

This content is provided to you freely by EdTech Books.

Access it online or download it at https://edtechbooks.org/general_college_chemistry_2/radioactive_decay.