Titrations II

Learning Objectives

By the end of this section, you will be able to:

Interpret titration curves for strong and weak acid-base systems
Compute sample pH at important stages of a titration

EXAMPLE 29.0.1

Titration of a Weak Acid with a Strong Base

Consider the titration of 25.00 mL of 0.100 M CH₃CO₂H with 0.100 M NaOH. The reaction can be represented as:

{CH}_{3} {CO}_{2} H + {OH}^{−} ⟶ {CH}_{3} {CO}_{2}^{−} + H_{2} O

Calculate the pH of the titration solution after the addition of the following volumes of NaOH titrant:

(a) 0.00 mL

(b) 25.00 mL

(d) 37.50 mL

Solution

(a) The initial pH is computed for the acetic acid solution in the usual ICE approach:

$K_{a} = \frac{[H_{3} O^{+}] [{CH}_{3} {CO}_{2}^{−}]}{[{CH}_{3} {CO}_{2} H]} \approx \frac{{[H_{3} O^{+}]}^{2}}{{[{CH}_{3} {CO}_{2} H]}_{0}},$ and $[H_{3} O^{+}] = \sqrt{K_{a} \times [{CH}_{3} {CO}_{2} H]} = \sqrt{1.8 \times 10^{−5} \times 0.100} = 1.3 \times 10^{−3}$

pH = −log (1.3 \times 10^{−3}) = 2.87

(b) The acid and titrant are both monoprotic and the sample and titrant solutions are equally concentrated; thus, this volume of titrant represents the equivalence point. Unlike the strong-acid example above, however, the reaction mixture in this case contains a weak conjugate base (acetate ion). The solution pH is computed considering the base ionization of acetate, which is present at a concentration of

\frac{0.00250 mol}{0.0500 L} = 0.0500 M {CH}_{3} {CO}_{2}^{−}

Base ionization of acetate is represented by the equation

{CH}_{3} {CO}_{2}^{−} (a q) + H_{2} O (l) ⇌ {CH}_{3} {CO}_{2} H (a q) + {OH}^{−} (a q)

K_{b} = \frac{[H^{+}] [{OH}^{−}]}{K_{a}} = \frac{K_{w}}{K_{a}} = \frac{1.0 \times 10^{−14}}{1.8 \times 10^{−5}} = 5.6 \times 10^{−10}

Assuming x << 0.0500, the pH may be calculated via the usual ICE approach: $K_{b} = \frac{x^{2}}{0.0500 M}$

x = [{OH}^{−}] = 5.3 \times 10^{- 6}

pOH = −log (5.3 \times 10^{- 6}) = 5.28

pH = 14.00 - 5.28 = 8.72

Note that the pH at the equivalence point of this titration is significantly greater than 7, as expected when titrating a weak acid with a strong base.

(c) Titrant volume = 12.50 mL. This volume represents one-half of the stoichiometric amount of titrant, and so one-half of the acetic acid has been neutralized to yield an equivalent amount of acetate ion. The concentrations of these conjugate acid-base partners, therefore, are equal. A convenient approach to computing the pH is use of the Henderson-Hasselbalch equation:

pH = p K_{a} + log \frac{[Base]}{[Acid]} = −log (K_{a}) + log \frac{[{CH}_{3} {CO}_{2}^{−}]}{[{CH}_{3} {CO}_{2} H]} = −log (1.8 \times 10^{−5}) + log (1)

pH = −log (1.8 \times 10^{- 5}) = 4.74

(pH = pK_a at the half-equivalence point in a titration of a weak acid)

(d) Titrant volume = 37.50 mL. This volume represents a stoichiometric excess of titrant, and a reaction solution containing both the titration product, acetate ion, and the excess strong titrant. In such solutions, the solution pH is determined primarily by the amount of excess strong base:

[{OH}^{−}] = \frac{(0.003750 mol - 0.00250 mol)}{0.06250 L} = 2.00 \times 10^{−2} M

pOH = −log (2.00 \times 10^{−2}) = 1.70, and pH = 14.00 - 1.70 = 12.30

Check Your Learning

Calculate the pH for the weak acid/strong base titration between 50.0 mL of 0.100 M HCOOH(aq) (formic acid) and 0.200 M NaOH (titrant) at the listed volumes of added base: 0.00 mL, 15.0 mL, 25.0 mL, and 30.0 mL.

Answer

0.00 mL: 2.37; 15.0 mL: 3.92; 25.00 mL: 8.29; 30.0 mL: 12.097

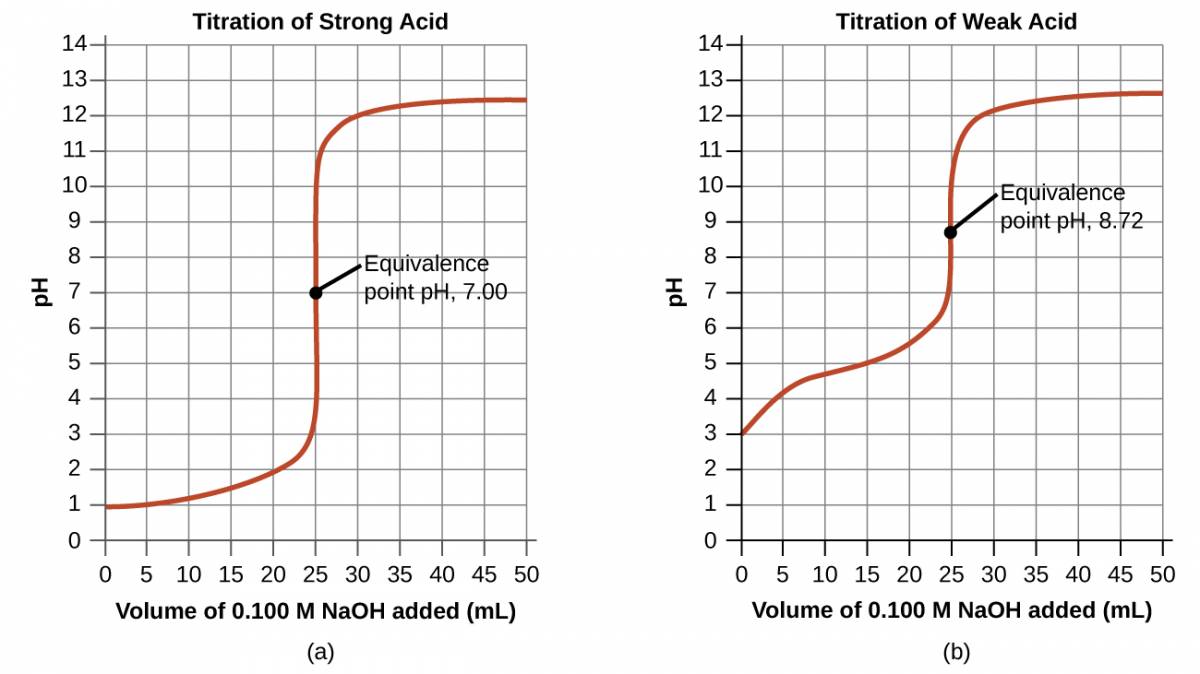
Performing calculations similar to those in the preceding example permits a more full assessment of titration curves. A summary of pH/volume data pairs for the strong and weak acid titrations is provided in Table 29.1 and plotted as titration curves in Figure 29.1. A comparison of these two curves illustrates several important concepts that are best addressed by identifying the four stages of a titration:

initial state (added titrant volume = 0 mL): pH is determined by the acid being titrated; because the two acid samples are equally concentrated, the weak acid will exhibit a greater initial pH

pre-equivalence point (0 mL < V < 25 mL): solution pH increases gradually and the acid is consumed by reaction with added titrant; composition includes unreacted acid and the reaction product, its conjugate base

equivalence point (V = 25 mL): a drastic rise in pH is observed as the solution composition transitions from acidic to either neutral (for the strong acid sample) or basic (for the weak acid sample), with pH determined by ionization of the conjugate base of the acid

postequivalence point (V > 25 mL): pH is determined by the amount of excess strong base titrant added; since both samples are titrated with the same titrant, both titration curves appear similar at this stage.

Table 29.1

pH Values in the Titrations of a Strong Acid and of a Weak Acid

Volume of 0.100 M NaOH Added (mL)	Moles of NaOH Added	pH Values 0.100 M HCl¹	pH Values 0.100 M CH₃CO₂H²
0.0	0.0	1.00	2.87
5.0	0.00050	1.18	4.14
10.0	0.00100	1.37	4.57
15.0	0.00150	1.60	4.92
20.0	0.00200	1.95	5.35
22.0	0.00220	2.20	5.61
24.0	0.00240	2.69	6.13
24.5	0.00245	3.00	6.44
24.9	0.00249	3.70	7.14
25.0	0.00250	7.00	8.72
25.1	0.00251	10.30	10.30
25.5	0.00255	11.00	11.00
26.0	0.00260	11.29	11.29
28.0	0.00280	11.75	11.75
30.0	0.00300	11.96	11.96
35.0	0.00350	12.22	12.22
40.0	0.00400	12.36	12.36
45.0	0.00450	12.46	12.46
50.0	0.00500	12.52	12.52

Figure 29.2

(a) The titration curve for the titration of 25.00 mL of 0.100 M HCl (strong acid) with 0.100 M NaOH (strong base) has an equivalence point of 7.00 pH. (b) The titration curve for the titration of 25.00 mL of 0.100 M acetic acid (weak acid) with 0.100 M NaOH (strong base) has an equivalence point of 8.72 pH.

Two graphs are shown. The first graph on the left is titled “Titration of Weak Acid.” The horizontal axis is labeled “Volume of 0.100 M N a O H added (m L).” Markings and vertical gridlines are provided every 5 units from 0 to 50. The vertical axis is labeled “p H” and is marked every 1 unis beginning at 0 extending to 14. A red curve is drawn on the graph which increases steadily from the point (0, 3) up to about (20, 5.5) after which the graph has a vertical section from (25, 7) up to (25, 11). The graph then levels off to a value of about 12.5 from about 40 m L up to 50 m L. The midpoint of the vertical segment of the curve is labeled “Equivalence point p H, 8.72.” The second graph on the right is titled “Titration of Strong Acid.” The horizontal axis is labeled “Volume of 0.100 M N a O H added (m L).” Markings and vertical gridlines are provided every 5 units from 0 to 50. The vertical axis is labeled “p H” and is marked every 1 units beginning at 0 extending to 14. A red curve is drawn on the graph which increases gradually from the point (0, 1) up to about (22.5, 2.2) after which the graph has a vertical section from (25, 4) up to nearly (25, 11). The graph then levels off to a value of about 12.4 from about 40 m L up to 50 m L. The midpoint of the vertical segment of the curve is labeled “Equivalence point p H, 7.00.”

29.0.2 Strong Acid + Weak Base

29.0.3 Weak Acid + Strong Base

29.0.4 Weak Acid Strong Base Titration

29.0.5 Weak Acid Titration Example

29.0.6 Strong Acid + Buffer

Previous Citation(s)

Flowers, P., et al. (2019). Chemistry: Atoms First 2e. https://openstax.org/details/books/chemistry-atoms-first-2e (14.7)

This content is provided to you freely by EdTech Books.

Access it online or download it at https://edtechbooks.org/general_college_chemistry_2/titrations_ii.